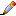|
|
|
Условие
Для каких $k$ можно закрасить на белой клетчатой плоскости несколько (конечное число, большее нуля) клеток в чёрный цвет так, чтобы на любой клетчатой вертикали, горизонтали и диагонали либо было ровно $k$ чёрных клеток, либо вовсе не было чёрных клеток?
Решение 1
Закрасим чёрным сначала $k$ клеток, стоящих подряд вдоль одной из диагоналей, идущей вправо-вниз. Затем сдвинем эту картинку по диагонали вправо-вверх на $k, 2k, 3k, ..., (k - 1)k$ клеток. Получится множество $A$ из $k^2$ чёрных клеток, которое каждая горизонталь и вертикаль пересекает не более чем по одной клетке, а каждая диагональ имеет с $A$ либо 0, либо $k$ общих клеток (рисунок слева для $k$ = 3). При этом всё множество $A$ лежит в квадрате $k^2\times k^2$.
Заметим, что если квадрат $n\times n$ сдвинуть на 2$n$ клеток по вертикали, то не существует диагонали, пересекающей оба эти квадрата (рисунок справа для $n$ = 3).
Поэтому, сдвинув множество $A$ на $2k^2, 4k^2, ..., 2(k-1)k^2$ вверх, мы получим множество $B$ из $k^3$ чёрных клеток, которое каждая горизонталь пересекает не более чем по одной клетке, а каждая вертикаль и диагональ имеет с $B$ либо 0, либо $k$ общих клеток. При этом все множество $B$ лежит в квадрате $2k^3\times 2k^3$.
Теперь, сдвинув множество $B$ на $4k^3, 8k^3, ..., 4(k-1)k^3$ вправо, мы получим искомое множество из $k^4$ чёрных клеток.
(Другими словами, построенное множество состоит из клеток с "координатами" $(- i+kj+4mk^3, i+kj+2nk^2), 0\leqslant i, j, m, n < k$.)
Решение 2
Есть 4 вида линий. Линии, на которых есть чёрные клетки, назовём покрываемыми. Требуется, чтобы на каждой покрываемой линии было ровно по $k$ чёрных клеток.
Набор чёрных клеток, для которого на каждой покрываемой линии содержится ровно $k$ клеток, назовём k-набором. Из $k$-набора можно получить 2$k$-набор. Для этого вырежем квадрат, содержащий
$k$-набор, и разместим его копии в квадратах, отмеченных буквами на рисунке.
Назовём $k$-набор супернабором, если его можно разбить на 1-наборы с тем же множеством покрываемых линий у каждого. Указанный выше метод из $k$-супернабора строит 2$k$-супернабор. Действительно, разобьём $k$-супернабор на 1-наборы. Возьмём один из них. Его копии на однобуквенных местах образуют 1-набор, который покрывает то же множество линий, что и 2$k$-набор. Весь
2$k$-набор разобьётся на такие 1-наборы, значит, это 2$k$-супернабор.
В $k$-супернаборе легко выделить $l$-набор для любого $l\leqslant k$: взять в нём $l$ разных 1-наборов с тем же множеством покрывающих линий у каждого. Осталось заметить, что 1-супернабор существует: он состоит, например, из одной клетки.
Ответ
Для всех натуральных $k$.
Замечания
1. В решении 1 получается $k^4$ клеток в квадрате со стороной порядка $4k^4$. В решении 2 – менее $4k^3$ клеток, порядок стороны – менее $k^3$.
2. 12 баллов.