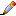|
|
|
Условие
Пусть $p$ и $q$ – взаимно простые натуральные числа. Лягушка прыгает по числовой прямой, начиная в точке $0$, каждый раз либо на $p$ вправо, либо на $q$ влево. Однажды лягушка вернулась в $0$. Докажите, что для любого натурального $d < p + q$ найдутся два числа, посещенные лягушкой и отличающиеся на $d$.Решение 1
Предположим, что для какого-то $d < p + q$ такие точки не найдутся.
Лемма. Найдутся такие целые $a$ и $b$, что $d = a p - b q$.
Доказательство леммы. Рассмотрим числа $a p - d$ при $a = 2, 3, \ldots, q + 1$. Если хотя бы одно из них делится на $q$, то есть имеет вид $b q$, то мы получаем $a p - d = b q$, что и требуется. В ином случае какие-то два их этих чисел дают одинаковый остаток от деления на $q$ (так как их всего ровно $q$ и остатка $0$ там нет). Тогда $(a_1 p - d) - (a_2 p - d) = q k$, откуда $p (a_1 - a_2) = q k$. Тогда, так как $p$ и $q$ взаимно просты, $a_1 - a_2$ кратно $q$; но в диапазоне от $2$ до $q + 1$ все числа отличаются менее чем на $q$, то есть этот случай невозможен. Лемма доказана.
Мы можем увеличить $a$ на $q$, а $b$ на $p$ – соотношение $d = a p - b q$ при этом не нарушится. Будем делать так до тех пор, пока не добьемся $a, b > 1$.
Пусть лягушка вернулась в $0$, сделав $n$ шагов вправо и $m$ шагов влево. Тогда $n p = m q$, а значит, $\frac{n}{m} = \frac{q}{p}$. Будем считать, что лягушка пропрыгивает эту последовательность $m + n$ ходов бесконечное число раз по циклу; ясно, что точки она при этом будет посещать те же.
Возьмем $k > \smash[t]{\frac{a + b}{m + n}}$. Расставим по кругу буквы, описывающие $(m + n) k$ подряд идущих ходов лягушки. Будем выписывать их по часовой стрелке, по одной букве на ход; если это ход вправо, напишем букву «П», а если ход влево – «Л». Всего мы расставили по кругу $n k$ букв «П» и $m k$ букв «Л».
Пусть мы найдем отрезок из $a + b$ подряд идущих букв, среди которых ровно $a$ раз встречается «П» (и ровно $b$ раз – «Л»). Тогда эти буквы соответствуют $a + b$ последовательным ходам, за которые лягушка сдвинулась ровно на $a p - b q = d$. Противоречие. Значит, ни на каком таком отрезке буква «П» не может встречаться $a$ раз.
Рассмотрим какой-то отрезок из $a + b$ подряд идущих букв. Пусть буква «П» встречается на нем не более чем $a - 1$ раз. Посмотрим на отрезок из $a + b$ букв, отличающийся от предыдущего сдвигом на $1$ по часовой стрелке, то есть получившийся выкидыванием одной буквы и добавлением другой. Заметим, что на новом отрезке буква «П» встречается не более чем $a - 1 + 1 = a$ раз, а так как ровно $a$ быть не может, то тоже не более чем $a - 1$ раз. Повторив эти рассуждения, получим, что на любом отрезке такой длины буква «П» встречается не более чем $a - 1$ раз. Мы можем рассмотреть среднее количество букв «П» во всех наборах $a+b$ подряд идущих букв и сделать вывод, что доля букв «П» во всем круге не более $\frac{a - 1}{a + b}$. Значит, отношение количества букв «П» к количеству букв «Л» во всем круге не превосходит $\frac{a - 1}{b + 1}$.
Аналогично, если на каком-то отрезке из $a + b$ подряд идущих букв буква «П» встречается не менее чем $a + 1$ раз, то отношение количества букв «П» во всем круге к количеству букв «Л» не менее $\frac{a + 1}{b - 1}$. Следовательно, $$\text{либо}\quad \frac{n k}{m k} \leq \frac{a - 1}{b + 1}, \quad\text{либо}\quad \frac{n k}{m k} \geq \frac{a + 1}{b - 1}.$$ При этом $\frac{nk}{mk} = \frac{n}{m} = \frac{q}{p}$. Чтобы прийти к противоречию, нам достаточно показать, что $$\frac{a - 1}{b + 1} < \frac{q}{p} < \frac{a + 1}{b - 1}.$$ Левое неравенство эквивалентно $(a - 1) p < (b + 1) q$, что следует из $a p - b q = d < p + q$. Правое неравенство аналогично эквивалентно $(a + 1) p > (b - 1) q$, что следует из $a p - b q = d > - p - q$.
Мы пришли к противоречию, значит, точки на расстоянии $d$ найдутся.
Решение 2
Случай $p=q=1$ очевиден. Иначе $p$ и $q$ различны, пусть $p < q$. Всего лягушка пропрыгала путь, длина которого делится на $p$ и на $q$, а значит, и на $pq$, так как $p$ и $q$ взаимно просты. Тогда длина пути равна $kpq$ для некоторого натурального $k,$ и лягушка сделала $kq$ «коротких» прыжков вправо и $kp$ «длинных» прыжков влево.
Как уже известно, что при взаимно простых $p$ и $q$ можно представить $d$ в виде $d = ap - bq$ с целыми $a$ и $b$. Это равенство, очевидно, сохранится, если одновременно увеличить (или уменьшить) $a$ на $q$ и $b$ на $p$. Поэтому можно выбрать $a$ натуральным и не превосходящим $q$. При этом $b$ будет неотрицательным (иначе $d \geqslant p+q$), и так как $a \leqslant q$, то $b < p$ (ведь $d>0$). Поэтому $a + b < p + q \leqslant k(p+q)$.
Назовём каждую серию из $a + b$ последовательных прыжков лягушки окном. Условно считаем, что за последним прыжком лягушки идёт её первый прыжок (как при движении по кругу), поэтому окно может состоять и из нескольких последних и первых прыжков. Тогда всего окон ровно $k(p + q)$ штук.
Надо найти окно, где лягушка сделала ровно $a$ коротких прыжков (и $b$ длинных) – тогда она сдвинется на $d$ за эти $a+b$ прыжков. Такое окно найдётся, если есть окно, где коротких прыжков не менее $a$, и окно, где их не более $a$: можно сдвигать первое окно по кругу, пока не дойдём до второго, число коротких прыжков в окне каждый раз меняется максимум на 1, поэтому будет момент, когда оно равно $a$.
Сложим число коротких прыжков во всех окнах – получим $kq(a + b)$, ведь каждый прыжок учли $a + b$ раз. Окон $k(p + q)$, и в среднем на окно придётся $\frac{kq(a + b)}{k(p+q)}$ коротких прыжков. Это число равно $$\frac{kq(a + b)}{k(p+q)}=\frac{qa + qb}{p+q}=\frac{pa+qa -d}{p+q}=a-\frac{d}{p+q},$$ что больше $a - 1$ и меньше $a$. Значит, найдётся окно, где коротких прыжков не менее $a$, и окно, где их не более $a$.
Решение 3
Как и в предыдущем решении, будем считать, что лягушка прыгает в бесконечном цикле. Также воспользуемся представлением $d = a p - b q$ для положительных $a$ и $b$, сумму $a + b$ обозначив за $r$.
За $\delta_{i}$ обозначим разность между положениями лягушки в момент $i + r$ (то есть через $i + r$ шагов после начала) и в момент $i$. Так как их разделяет $r$ шагов, то $$ \delta_{i} = x p - (r - x) q = a p + (x - a) p - b q - (r - x - b) q= $$ $$ = d + (x - a) p + (x - (r - b)) q = d + (x - a) (p + q).$$ Если $\delta_{i}$ равно $d$, то мы нашли искомые позиции. Предположим противное: пусть $\delta_{i} \neq d$ для всех $i$. Тогда все числа $\delta_{i}$ имеют вид $d + (p + q) k$ для целых $k \neq 0$.
Заметим, что разность между $\delta_{i}$ и $\delta_{i + 1}$ определяется тем, какими были $(i + 1)$-й и $(i + r + 1)$-й шаги; разобрав случаи, нетрудно убедиться, что она равна $-(p + q)$, $0$ или $p + q$. Это означает, что числа $\delta_{i}$ либо все меньше $0$ (имеют вид $d - (p + q) k$ для натурального $k$), либо все больше $0$ (имеют вид $d + (p + q) k$ для натурального $k$).
Тогда рассмотрим позицию лягушки через $r T$ шагов, где $T$ – количество шагов в ее цикле. С одной стороны, она равна сумме $\delta_{0} + \delta_{r} + \delta_{2r} + \ldots + \delta_{r(T-1)}$, которая по доказанному выше должна быть либо отрицательной, либо положительной. С другой стороны, через $r T$ шагов лягушка вернется на позицию $0$. Противоречие.
Решение 4
Лягушку из условия назовём старой. Будем считать, что она пропрыгивает свою последовательность ходов бесконечное число раз по циклу. Посадим на прямую новую лягушку в точку $d$ и заставим её прыгать ту же последовательность прыжков, что прыгает старая (тоже в бесконечном цикле).
Множество чисел, посещённых новой лягушкой, получается из множества чисел, посещённых старой, сдвигом на $d$. Если хотя бы одно число из нового множества совпадет с числом из старого, то обратный сдвиг даст нам искомую пару чисел. Предположим, что этого не произойдёт.
Как и в предыдущем решении, представим число $d$ в виде $a p - b q$ для некоторых неотрицательных $a$ и $b$. Заставим старую лягушку пропрыгать $a + b$ ходов по её циклу; она окажется в точке $e = x p - y q$, где $x + y = a + b$. Так как $a - x = y - b$, разность координат новой и старой лягушек кратна $p + q$: $d - e = (a - x) p - (b - y) q = (a - x) (p + q)$.
Далее пустим лягушек прыгать одновременно: старую по продолжению исходной траектории, а новую – по сдвинутой. На каждом шаге разность их координат будет либо не меняться (если они прыгают в одну сторону), либо меняться на $p + q$ (если одна прыгает на $+p$, а другая на $-q$). Таким образом, разность всегда будет оставаться кратной $p + q$; при этом она, по предположению, не может становиться нулевой, поэтому она всегда будет сохранять знак.
Пусть лягушки пропрыгали полный цикл и вернулись (новая в $d$, а старая в $e$). Количество ходов в цикле обозначим через $T$. Сумму всех чисел, посещённых новой лягушкой (без учёта начальной позиции), обозначим через $S_1$, а сумму чисел, посещённых старой, – через $S$. С одной стороны, числа на соответствующих ходах отличались не менее чем на $p + q$, причём разность всегда имела один и тот же знак, поэтому $\lvert S_1 - S \rvert \geq T (p + q)$. С другой стороны, набор чисел, посещённых новой лягушкой за цикл, отличается от аналогичного набора старой лягушки сдвигом на $d$, поэтому $\lvert S_1 - S \rvert = Td$ (отметим, что эти наборы могут содержать некоторые числа по несколько раз, если в течение цикла лягушка посещала их неоднократно). Подставляя и сокращая на $T$, получаем $d \geq p + q$, что противоречит условию задачи.
Решение 5
Пусть в момент времени $k$ лягушка находится в точке $a_k$, $a_0 = a_N = 0$. Продолжим последовательность $(a_i)$ периодически по правилу $a_{i+N} = a_i$. Обозначим $A = p+q$. Заметим, что $-q \equiv p \bmod A$, поэтому $a_n \equiv n p \bmod A$ для любого $n$.
Так как $p$ и $q$ взаимно простые, то $p$ и $A$ взаимно простые. Докажем, что найдется такое целое $s$, что $sp \equiv d \bmod A$.
В самом деле, числа $0, p, 2p, \dots, (A-1)p$ дают различные остатки при делении на $A$ (иначе для некоторых $ 0 \leq i < j < A $ получаем, что $(j-i)p \equiv 0 \bmod A$, чего не может быть, так как $j - i$ не делится на $A$, а $p$ взаимно просто с $A$). А значит, среди этих остатков есть и $d$.
Обозначим $r_k = a_{s+k} - a_k$. Легко видеть, что все $r_k$ дают остаток $d$ от деления на $A$.
Если $a_k$ – самая левая из точек, посещенных лягушкой, то $r_k > 0$. Если $a_k$ – самая правая точка, то $r_k < 0$. Значит, при некотором $i$ в последовательности $r_i$ происходит перемена знака, $r_i < 0$ и $r_{i+1} > 0$. Тогда $r_{i+1} < A$, потому что $$r_{i+1} - r_i = (a_{i+s+1} - a_{i+s}) - (a_{i+1} - a_i) \leqslant p - (-q) = A.$$ А так как $r_{i+1} \equiv d \bmod A$, то $r_{i+1} = d$, что и требовалось.
Решение 6
Поскольку $p$ и $q$ взаимно просты, лягушка может вернуться в исходную точку, только сделав $kq$ прыжков вправо и $kp$ прыжков влево, где $k$ – натуральное число. Изобразим путь $P$ лягушки на целочисленной решетке так: когда лягушка прыгает (на $p$) вправо будем сдвигаться на 1 вправо, а когда прыгает влево – на 1 вверх. Ниже на рисунке слева изображен такой путь $P$ для $p = 7$, $q = 11$, $k = 1$ и последовательности прыжков $7 - 11 + 7 - 11 + 7 + 7 - 11 + 7 - 11 + 7 + 7 - 11 + 7 - 11 + 7 + 7 - 11 + 7 = 0$.
Как известно, найдутся натуральные $a$ и $b$, для которых $d = pa - qb$. Сдвинув путь $P$ на $a$ вправо и на $b$ вверх, получим новый путь $Q$. Выше на рисунке справа изображён путь $Q$, полученный из пути на левом рисунке для $d = 10$, $a = 3$ и $b = 1$ ($10 = 7\cdot3 - 11\cdot1$). Если $P$ и $Q$ имеют общую точку $(x, y)$, то точка $(x - a, y - b)$ также лежит на $P$. Соответствующие положения лягушки на числовой прямой равны $p(x - a) - q(y - b)$ и $px - qy$, а $(px - qy) - (p(x - a) - q(y - b)) = pa - qb = d$, что и требовалось. То же будет верно, если путь $Q$ имеет общую точку с расширенным путем ${\bf P}$, полученным добавлением к $P$ его копий, полученными сдвигами на $(kq, kp)$, $(2kq, 2kp)$ и т.д.
Предположим, что общих точек у путей ${\bf P}$ и $Q$ нет, например, $Q$ лежит ниже ${\bf P}$. На рисунке справа ${\bf P}$ состоит из двух копий $P$, а $Q$ получен из $P$ сдвигом, соответствующим $d = 20$, $a = 6$, $b = 2$ ($20 = 7\cdot6 - 11\cdot2$).
Рассмотрим заштрихованную фигуру $F$, расположенную «между» ${\bf P}$ и $Q$, и наименьший содержащий её прямоугольник (его размеры $kq\times(kp+l)$, где $l$ – натуральное число). Когда $Q$ совпадает с $P$, площадь $S(F)$ равна 0. Сдвиг на $a$ вправо увеличил эту площадь на $kpa$, а сдвиг на $b$ вверх уменьшил её на $kqb$. Значит, $S(F) = k(pa - qb) = kd$.
Оценим площадь $F$ снизу другим способом. Фигуру $F$ можно разбить на $kq$ вертикальных полосок толщиной в одну клетку. В каждой полоске есть минимум одна клетка (нижняя). Фигуру $F$ пересекают по внутренним отрезкам $kp + l - 1$ горизонтальных линий сетки. В каждой вертикальной полоске клеток хотя бы на одну больше, чем количество пересекающих её линий, т.к. есть клетка прямо под каждой линией, и клетка выше самой верхней линии. Значит, общая площадь $F$ не менее $kq + kp + l - 1$ клеток, что не меньше $k(p + q)$ клеток. Это противоречит неравенству $d < p + q$.
Источники и прецеденты использования
| олимпиада | |
| Название | Московская математическая олимпиада |
| год | |
| Номер | 84 |
| Год | 2021 |
| класс | |
| Класс | 9 |
| задача | |
| Номер | 6 |
| олимпиада | |
| Название | Московская математическая олимпиада |
| год | |
| Номер | 84 |
| Год | 2021 |
| класс | |
| Класс | 10 |
| задача | |
| Номер | 5 |
| олимпиада | |
| Название | Турнир городов |
| год/номер | |
| Номер | 42 |
| Дата | 2020/21 |
| вариант | |
| Вариант | весенний тур, сложный вариант, 8-9 класс |
| задача | |
| Номер | 7 |