Краткий справочник математических терминов

В этом кратком справочнике поясняются понятия и теоремы, упоминаемые в книгах и задачах, опубликованных на нашем сайте. Справочник ни в кой мере претендует на полноту — это лишь необходимый комментарий к нашим задачам. Справочник формируется в соответствии с запросами наших читателей. Если Вас интересует, что означает данный термин, или что утверждает данная теорема, заполните форму, и мы ответим на Ваш вопрос.

Знаком "*" помечены факты, относящиеся к данному понятию, знаком "-" помечены варианты формулировки определений.

А Б В Г Д З И К Л М Н О П Р С Т У Ф Х Ц Ч Э

Статьи на букву 'С':

Сегмент
- круговой
  Круговым сегментом называется пересечение круга и полуплоскости при условии, что это пересечение содержит более одной точки.
  * Площадь кругового сегмента, не равного полукругу, вычисляется по формуле S = ${\frac{\pi R^{2}}{360}}$ $\alpha$ ± S, где R — радиус круга, $\alpha$ — градусная мера соответствующего центрального угла, а S — площадь треугольника, с вершинами в центре круга и в концах радиусов, ограничивающих соответствующий сектор. Знак "+" берётся, когда $\alpha$ > 180^o, а знак "-" — когда $\alpha$ < 180^o. Площадь полукруга равна $\pi$ R²/2.

Сектор
- круговой
  Круговым сектором называется пересечение круга и центрального угла (с несовпадающими сторонами) с вершиной в центре данного круга. Даный центральный угол называется соответствующим данному сектору или ограничивающим данный сектор.
  * Если S — площадь кругового сектора, R — радиус круга, а $\alpha$ — градусная мера соответствующего центрального угла, то S = ${\frac{\pi R^{2}}{360}}$ $\alpha$ .

Секущая
Прямая c, пересекающая прямые a и b называется их секущей. Пусть A и B — различные точки пересечения прямой c с прямыми a и b соответственно, точка P лежит на прямой a, а точка Q на прямой b. Если точки P и Q расположены в разных полуплоскостях относительно прямой c, то углы PAB и QBA называются внутренними накрест лежащими. Если же точки P и Q расположены в одной полуплоскости относительно прямой c, то углы PAB и QBA называются внутренними односторонними.

Серединный перпендикуляр
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
* Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудаленных от конца данного отрезка.

Симедиана
Пусть AM — медиана треугольника ABC, а прямая AS симметрична прямой AM относительно биссектрисы угла A (точка S лежит на отрезке BC). Тогда отрезок AS называют симедианойтреугольника ABC; иногда симедианой называется луч AS.
* Симедианы треугольника пересекаются в точке, изогонально сопряженной точке пересечения медиан.
Точку пересечения симедиан треугольника называют точкой Лемуана.

Симметрия
- осевая
  Симметрией относительно прямой l (обозначение: S_l) называют преобразование плоскости, оставляющее все точки прямой l на месте, и переводящее каждую точку X, не лежащую на l, в такую точку X', что l — серединный перпендикуляр к отрезку XX'. Это преобразование называют также осевой симметрией, а l —осью симметрии.
  Если фигура переходит в себя при симметрии относительно прямой l, то l называют осью симметрии этой фигуры.
- относительно прямой
  См. "симметрия осевая".
- относительно точки
  См. "симметрия центральная".
- скользящая
  Скользящей симметрией называют композицию симметрии относительно некоторой прямой l и переноса на вектор, параллельный l (этот вектор может быть и нулевым).
- центральная
  Симметрией относительно точки A называют преобразование плоскости, переводящее точку X в такую точку X', что A — середина отрезка XX'. Другие названия этого преобразования — центральная симметрия с центром A или просто симметрия с центром A.
  * Заметим, что симметрия с центром A представляет собой частный случай двух других преобразований — она является поворотом на 180^o с центром A, а также гомотетией с центром A и коэффициентом -1.
  * Если M'(x';y') — точка, симметричная точке M(x;y) относительно точки O(a;b), то x' = 2a - x, y' = 2b - y (запись в декартовых координатах на плоскости).
  Если фигура переходит в себя при симметрии относительно точки A, то A называют центром симметрии этой фигуры.
  Центральную симметрию с центром в точке A часто обозначают через S_A или Z_A.

Сопряжённые диаметры
- гиперболы
  Сопряжёнными диаметрами гиперболы называют пару её диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
- эллипса
  Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
  * Если эллипс является образом окружности при аффинном преобразовании, то его сопряжённые диаметры являются образами двух перпендикулярных диаметров этой окружности.
  см. задачу 58474

Cреднее степенное
Для любого действительного α ≠ 0 средним степенным положительных чисел x₁ , x₂ , . . . , x_n порядка α называется число

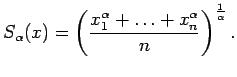
$\displaystyle S_{\alpha}(x)=\left(\dfrac{x_1^{\alpha}+\ldots+x_n^{\alpha}}{n} \right)^{\frac{1}{\alpha}}.$

Частными случаями средних степенных являются: среднее гармоническое (α = -1), среднее арифметическое (α = 1), среднее квадратичное (α = 2).
Средним степенным порядка 0 будем считать среднее геометрическое $S_0(x)=\sqrt[n]{x_1\ldots x_n}$ .
* Если α < β, то S_α(x₁ , x₂ , . . . , x_n) ≤ S_β(x₁ , x₂ , . . . , x_n) (смотри задачи 61413 и 61414).

Средняя линия
- трапеции
  Средней линией трапеции называется отрезок, соединяющий середины боковых сторон данной трапеции.
  * Средняя линия трапеции параллельна основаниям трапеции, а ее длина равна полусумме длин оснований трапеции. (См. задачу 54165.)
- треугольника
  Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
  * Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине. (См. задачу 54117.)
  * Средняя линия треугольника, соединяющая середины двух данных сторон, и медиана, проведённая к третьей стороне, делят друг друга пополам.

Cтепень
- инверсии
  см. "инверсия на плоскости".
- точки относительно окружности
  Рассмотрим окружность S и точку P на плоскости. Пусть прямая, проведенная через точку P, пересекает окружность в точках A и B. Тогда произведение PA^.PB не зависит от выбора прямой. Эта величина, взятая со знаком плюс для точки P вне окружности и со знаком минус для точки P внутри окружности, называется степенью точки P относительно окружности S.

Стереографическая проекция
Рассмотрим в пространстве единичную сферу с центром в начале координат. Пусть N(0, 0, 1) — ее северный полюс. Стереографической проекцией сферы на плоскость называют отображение, которое каждой, отличной от N, точке M сферы сопоставляет точку пересечения прямой MN с плоскостью Oxy.
* При стереографической проекции окружности на сфере, не проходящие через северный полюс, переходят в окружность на плоскости, а окружности, проходящие через северный полюс, переходят в прямые на плоскости.

От кого (e-mail):
Что Вас интересует: