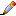|
|
|
Условие
Поверхность выпуклого многогранника A1B1C1A2B2C2 состоит из восьми треугольных граней AiBjCk, где i, j, k меняются от 1 до 2. Сфера с центром в точке O касается всех этих граней. Докажите, что точка O и середины трёх отрезков A1A2, B1B2 и C1C2 лежат в одной плоскости.
Решение
Пусть A, B и C – середины отрезков A1A2, B1B2 и C1C2 соответственно. Нужно доказать, что векторы и
компланарны.
Пусть P1, P2, ..., P8 – точки касания сферы с гранями многогранника, а S1, S2, ..., S8 –
площади соответствующих граней. Обозначим через R радиус этой сферы. Докажем два вспомогательных утверждения.
Утверждение 1.
Доказательство. Пусть u – произвольный единичный вектор, а натуральное число q меняется от 1 до 8. Тогда где αq – угол между векторами
u и
Число Sq cos αq по модулю равно площади ортогональной проекции q-й грани многогранника A1B1C1A2B2C2 на плоскость π, ортогональную вектору u, имеет знак "–", если векторы u и
образуют тупой угол, и знак "+" иначе.
Следовательно, скалярное произведение вектора на вектор
u равно RS, где S – сумма площадей проекций всех граней многогранника на плоскость π, в которой каждая из этих площадей берётся со знаком "+" или "–" в зависимости от того, острый или тупой угол образуют векторы u и
Примем направление вектора u за направление "вверх". Каждая точка внутри ортогональной проекции многогранника
A1B1C1A2B2C2 на плоскость π дважды покроется проекциями его граней на эту плоскость: один раз проекцией "верхней" грани и один раз "нижней". Площади этих двух проекций брались в сумме S с разными знаками: "+" и "–" соответственно. Поэтому площадь проекции многогранника на плоскость π равна сумме площадей проекций всех его "верхних" граней. Она также равна сумме площадей проекций всех его "нижних" граней, а S равно разности этих сумм, то есть нулю.
Следовательно, скалярное произведение вектора w на произвольный единичный вектор u равно нулю. Значит, сам вектор
w равен нулю.
Утверждение 2. При всех q = 1, 2, ..., 8 имеет место равенство где Pq – точка касания сферы с гранью AiBjCk,
Sq,1, Sq,2 и
Sq,3 – площади треугольников PqBjCk, AiPqCk и AiBjPq соответственно.
Доказательство.
Покажем, что сумма во второй скобке равна 0. Для этого
рассмотрим её проекцию на прямую, перпендикулярную к AiPq. Вектор спроектируется в нулевой вектор, проекция вектора
будет равна вектору
, а проекция вектора
будет равна вектору
(см. рис.). Площади Sq,2 и Sq,3 относятся как высоты CkK и BjL соответствующих треугольников с общим основанием. Следовательно,
Sq,2·BjL = Sq,3·CkK. Значит, векторы и
противоположны. Отсюда получаем, что сумма
параллельна прямой AiPq. Аналогично доказывается, что эта сумма параллельна прямым BjPq и CkPq. Таким образом, эта сумма равна нулевому вектору.
По утверждению 1 С помощью утверждения 2 преобразуем каждое слагаемое этой суммы в сумму вида
а затем сгруппируем коэффициенты при одинаковых векторах. Получим равенство
где k1 – сумма площадей треугольников PqBjCk, лежащих в одной плоскости с точкой A1, аналогично определяются остальные коэффициенты. Заметим, что k1 = k2, ведь каждые два треугольника вида PqBjCk с общей стороной
BjCk симметричны друг другу относительно биссекторной плоскости двугранного угла при ребре
BjCk. Аналогично доказываются равенства l1 = l2 и
m1 = m2. Отсюда
где k1, l1, m1 – положительные числа. Следовательно, векторы
и
компланарны.
Замечания
Эта задача является трёхмерным аналогом известной планиметрической теоремы Ньютона – см. задачу 55451.